HIMPUNAN I
1.1.
DEFINISI
Himpunan merupakan kumpulan objek-objek yang berbeda. Himpunan
adalah kumpulan objek yang didefinisikan secara jelas dalam sembarang urutan. Himpunan adalah kumpulan dari objek-objek tertentu yang tercakup dalam
satu kesatuan dengan keterangannya yang jelas. Untuk menyatakan suatu himpunan,
digunakan huruf besar / KAPITAL seperti A, B, C dsb. Sedangkan untuk menyatakan
anggota-anggotanya digunakan huruf kecil seperti a, b, c, dsb. Konsep
himpunan merupakan konsep dasar dalam aritmatika. Objek milik himpunan disebut
anggota atau elemen himpunan. Jika p adalah anggota himpunan A, ditulis p Î A. Sebaliknya jika p adalah
bukan anggota himpunan A, maka ditulis p Ï A.
1.2
PENYAJIAN HIMPUNAN
Ada 4 cara untuk menyatakan suatu himpunan, yaitu:
1.
Enumerasi
Mengenumerasi
artinya menulis semua elemen himpunan yang bersangkutan di antara dua buah
tanda kurung kurawal. Biasanya himpunan diberi nama dengan menggunakan huruf
kapital maupun dengan menggunakan simbol-simbol lainnya.
Contoh:
1. Himpunan A berisi empat bilangan asli.
Dapat ditulis sebagai berikut A = {1,2,3,4}
2. Himpunan B berisi lima
bilangan genap positif pertama.
Dapat ditulis sebagai
berikut B = { 2,4,6,8,10}
3. Himpunan C berisi 100 buah bilangan asli pertama.
Dapat ditulis sebagai
berikut C = {1, 2, ..., 100 }
4. Himpunan Z berisi bilangan bulat.
Dapat
ditulis sebagai berikut Z = {…, -2, -1, 0, 1, 2, …}.
Keanggotaan
x
Î
A : x merupakan anggota himpunan A;
x
Ï
A : x bukan merupakan anggota himpunan A.
Contoh:
Misalkan:
A = {1, 2, 3, 4}, R
= { a, b, {a, b, c}, {a, c} }
K = {{}}
maka
3 Î A
{a, b, c} Î
R
c Ï R
{} Î
K
{} Ï R
2. Simbol-simbol Baku
Beberapa simbol baku yang biasa digunakan untuk
mendefinisikan himpunan antara lain:
P = himpunan bilangan
bulat positif.
N = himpunan bilangan
alami (natural).
Z = himpunan bilangan
bulat
Q = himpunan bilangan rasional
R = himpunan bilangan riil
C = himpunan bilangan kompleks
U = himpunan semesta
3. Notasi Pembentuk Bilangan
Himpunan dinyatakan dengan menulis syarat yang harus
dipenuhi anggotanya.
Notasi: { x | syarat yang harus dipenuhi oleh x }
Aturan dalam penulisan syarat keanggotaan:
a. Bagian di kiri tanda ‘|’
melambangkan elemen himpunan
b. Tanda ‘|’ dibaca dimana atau sedemikian sehingga
c. Bagian di kanan tanda
‘|’ menunjukan syarat keanggotaan himpunan
d. Setiap tanda ‘,’ di
dalam syarat keanggotaan dibaca dan
Contoh:
1. A adalah himpunan
bilangan bulat positif yang lebih kecil dari 5.
Dinyatakan sebagai:
A = { x | x adalah
himpunan bilangan bulat posif lebih kecil dari 5}
Notasi
matematikanya:
A = { x | x Î P, x < 5 }
Yang ekivalen
dengan A = { 1, 2, 3, 4 }
2. B adalah himpunan
bilangan genap positif yang lebih kecil atau sama dengan 8.
Dinyatakan sebagai:
B = { x | x adalah
himpunan bilangan genap positif yang lebih kecil dari 8 }
Notasi Matematikanya:
B = { x | x/2 Î
P, 2 < x < 8 }
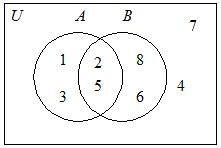
4. Diagram Venn
Diagram
Venn menyajikan himpunan secara grafis. Didalam diagram Venn, himpunan semesta
(U) digambarkan sebagai suatu segi empat sedangkan himpunan lainnya digambarkan
sebagai lingkaran di dalam segi empat tersebut.
Contoh:
Misalkan
U = {1, 2, …, 7, 8},
A =
{1, 2, 3, 5} dan
B = {2, 5, 6, 8}.
Diagram
Venn:
1.3. DEFINISI PADA TEORI HIMPUNAN
1. Kardinalitas
Jumlah
elemen di dalam A disebut kardinal
dari himpunan A.
Notasi:
n(A)
atau êA ê
Contoh:
(i) B = { x | x merupakan bilangan
prima yang lebih kecil dari 20 },
atau B
= {2, 3, 5, 7, 11, 13, 17, 19}
maka
½B½ = 8
(ii) T =
{kucing, a, Amir, 10, paku},
maka ½T½ = 5
(iii) A = {a,
{a}, {{a}} },
maka ½A½ = 3
2. Himpunan Kosong
Himpunan kosong adalah himpunan yang tidak mempunyai
elemen.
Notasi : Æ atau {}
Contoh:
(i) E
= { x | x < x }, maka n(E) = 0
(ii) P =
{ orang Indonesia yang pernah ke bulan }, maka n(P ) = 0
(iii) A = {x
| x adalah akar persamaan kuadrat x2 + 1 = 0 }, n(A)
= 0
Himpunan { { } } dapat
juga ditulis sebagai { Æ }
Himpunan {{ }, {{ }}}
dapat juga ditulis sebagai {Æ, {Æ}}
{Æ} bukan himpunan kosong karena ia memuat satu elemen yaitu himpunan kosong.
3.
Himpunan Bagian (Subset)
Himpunan A
dikatakan himpunan bagian dari himpunan B
jika dan hanya jika setiap elemen A
merupakan elemen dari B.
Dalam hal ini, B
dikatakan superset dari A.
Notasi:
A
Í B
Diagram Venn A Í B:
Contoh:
(i) { 1, 2, 3} Í {1, 2, 3, 4, 5}
(ii)
{1, 2, 3} Í {1,
2, 3}
· A dan A A, maka dan A disebut himpunan bagian tak sebenarnya
(improper subset) dari himpunan A.
Contoh:
A = {1, 2, 3}, maka {1, 2, 3} dan Æ adalah improper subset dari A.
· A Í B
berbeda dengan A Ì B
(i)
A Ì B : A adalah himpunan bagian
dari B tetapi A ¹ B.
A adalah himpunan bagian sebenarnya (proper subset) dari B.
Contoh: {1} dan
{2, 3} adalah proper subset dari {1, 2, 3}
(ii) A Í B : digunakan untuk menyatakan bahwa A adalah himpunan bagian (subset) dari B
yang memungkinkan A = B.
4. Himpunan yang Sama
·
A = B jika dan
hanya jika setiap elemen A merupakan
elemen B dan sebaliknya setiap elemen
B merupakan elemen A.
·
A = B
jika A
adalah himpunan bagian dari B dan B adalah himpunan bagian dari A.
Jika tidak demikian, maka A ¹ B.
Notasi
: A = B « A
Í B dan B Í A
Contoh:
(i) Jika A = { 0, 1 } dan B = { x | x (x
– 1) = 0 }, maka A = B
(ii) Jika A = { 3, 5, 8, 5 } dan B = {5, 3, 8 }, maka A = B
(iii) Jika A =
{ 3, 5, 8, 5 } dan B = {3, 8}, maka A ¹ B
Untuk tiga buah
himpunan, A, B, dan C berlaku aksioma
berikut:
(a) A = A, B = B,
dan C = C
(b) jika A = B,
maka B = A
(c) jika A = B
dan B = C, maka A = C
5. Himpunan terhingga
Himpunan terhingga adalah himpunan yang banyak
anggotannya terhingga.
Contoh:
D = {x | x adalah bilangan asli yang kurang dari 11}
D adalah himpunan terhingga, karena elemen-elemennya
terhingga yaitu 1, 2, 3, 4, 5, 6, 7, 8, 9, 10.
6. Himpunan tak hingga
Himpunan
tak hingga adalah himpunan yang banyak anggotanya tidak terhingga atau tidak
terbatas.
Contoh:
Z = {y | y adalah bilangan asli}
Z
adalah himpunan tak hingga, karena elemen-elemennya tidak terbatas atau tak
berhingga.
7. Himpunan Ekivalen
Himpunan
A dikatakan ekivalen dengan himpunan B jika dan hanya jika kardinal dari
kedua himpunan tersebut sama.
Notasi
: A ~ B « ½A½ = ½B½
Contoh:
Misal
A = { 1, 3, 5, 7 } dan B = { a, b, c, d
}, maka A ~ B sebab ½A½ = ½B½ = 4
8. Himpunan Saling Lepas
Dua
himpunan A dan B dikatakan saling lepas (disjoint)
jika keduanya tidak memiliki elemen yang sama.
Notasi
: A // B
Diagram Venn:
Contoh: Jika
A = { x | x P, x < 8 } dan B = { 10, 20, 30, ... }, maka A // B.
9. Himpunan Kuasa (power set)
Himpunan
kuasa adalah himpunan seluruh himpunan bagian dari suatu himpunan. Himpunan
kuasa dari himpunan A adalah suatu himpunan yang elemennya merupakan semua
himpunan bagian dari A, termasuk himpunan kosong dan himpunan A sendiri.
Notasi : P (A)
atau 2A
Contoh1:
Jika A = { 1, 2
}, maka P (A) = { , { 1 }, { 2 }, { 1, 2 }}
Contoh2:
Himpunan kuasa dari himpunan kosong adalah P (Æ) = {Æ}, dan himpunan kuasa dari himpunan {Æ} adalah P({Æ}) = {Æ, {Æ}}.
1.4. OPERASI – OPERASI DASAR HIMPUNAN
1.
Irisan (Perpotongan / Intersection)
Irisan
himpunan A dan himpunan B adalah himpunan yang setiap elemennya merupakan
elemendari himpunan A dan himpunan B. Irisan dinyatakan dengan A Ç
B yang dibaca ”A irisan B”.
Diagram
Venn untuk A Ç
B
Contoh:
S = {a, b, c, d} dan T = {b,
d, f, g}
Maka S Ç
T = {b, d}
Dapat dinyatakan dengan A Ç
B = {x | x Î
A dan x Î
B}
Setiap
himpunan A dan himpunan B mengandung A Ç B sebagai subhimpunan, yaitu
(A Ç
B) Ì A dan (A Ç B) Ì B
Jika
himpunan A dan himpunan B tidak mempunyai elemen-elemen yang dimiliki bersama,
berarti A dan B terpisah, maka irisan dari keduanya adalah himpunan kosong.
2. Gabungan (Perpaduan /
Union )
Gabungan
(Union ) himpunan dari A dan B adalah himpunan
yang setiap anggotanya merupakan anggota himpunan A atau B atau keduanya. Union
tersebut dapat dinyatakan sebagai A È B dibaca A union B.
Diagram
venn dari A È
B
Contoh
A = {a, b, c, d} dan B = {e,
f, g}
Maka A È
B = {a, b, c, d, e, f, g}
A È B = {x | x Î A atau x Î B}
Berlaku hukum A È B = B È A
A dan B kedua-duanya juga selalu berupa subhimpunan dari A È B, yaitu
A Ì
(A È
B) dan B Ì
(A È
B)
3.
Komplemen (complement)
Komplemen
dari suatu himpunan A terhadap himpunan semesta U adalah suatu himpunan yang
elemennya merupakan elemem U yang bukan elemen A, yaitu selisih dari himpunan
semesta U dan A. Komplemen dapat didefinisikan secara ringkas sebagai berikut
A’ = {x |
x Î
U dan x Ï
A} atau A’ = {x |
x Ï
A}
Diagram Venn dari A’.
Contoh:
Misalkan U = {1,2,3,…,9}
A = {1,3,7,9} carilah
A’ !
JAWAB
A’
= {2,4,6,8}
4.
Selisih (difference)
Selisih
dari himpunan A dan B adalah suatu himpunan yang elemennya merupakan elemen A
dan bukan elemen B. Dinyatakan dengan A – B dibaca ”selisih A dan B” atau ”A
kurang B”. Himpunan A
mengandung A – B sebagai subhimpunan, berarti(A – B) Ì A.
Diagram Venn untuk A – B
Contoh:
Jika A = { 1,2,3,...10} dan B = { 2,4,6,8,10} Carilah A –
B dan B – A!
Jawab
A – B = { 1,3,5,7,9}
B – A = 0 {himpunan kosong}
5.
Beda Setangkup (symmetric difference
/ Selisih simetri)
Beda setangkup dari himpunan A dan B adalah suatu
himpunan yang elemennya ada pada himpunan A dan B tetapi tidak pada keduanya.
Diagram Venn untuk A B
Contoh:
Jika A = { 2, 4,6} dan B = { 2,3,5} Carilah A B!
Jawab
A B = { 3,4,5,6}
Latihan:
1. Jika
A = {2, 4, 6, 8, 10} dan B = {4, 10, 14, 18} carilah A Ç B!
2. Jika
A = { 2, 5, 8 , 10} dan B = { 7, 5, 22 }, carilah A È B!
3. Misalkan
U = { 1, 2, 3, ..., 10 }, jika A = {1, 3, 5, 7, 9}, carilah A’!
4. Jika
A = { 1, 2, 3, ..., 10 } dan B = { 2, 4, 6, 8}, carilah A – B!
5. Jika
A = {1, 2, 4, 6 } dan B = { 2, 3, 5,7 }, carilah A Å B!
6. Jika U= {a, b, c, . . . i}, A= { a, i}, B= {a, b, c} , dan C= {a, g, h}.
Carilah:
a) A Ç B
Ç C
b) A È (B
Ç C)
c) AÈ B ÈC
d) A′
Ç (BÈ C)
e) (A
ÈB) Ç C′